【www.zhangdahai.com--其他范文】
龚京风,郑文利,宣领宽,徐宗著
(武汉科技大学汽车与交通工程学院,湖北 武汉,430065)
功能梯度材料(FGMs)已广泛应用于航空航天[1-2]、汽车工业[3-4]等领域,其中很多应用环境存在高温和温度梯度较大的情况,因此开发求解FGMs热弹性问题的数值模拟方法,为FGMs的热力学性能分析提供有效手段具有重要意义。
针对FGMs的热弹性问题,目前常用的分析方法为有限元法(FEM),但由于FGMs的组成和结构具有空间梯度,FEM计算结果可能会出现应力分布不连续的现象[5]。Kim等[6]采用八节点四边形单元(Q8)改进FEM,但仍不能完全解决上述问题。而另一方面,有限体积法(FVM)在计算力学中的应用也得到研究人员的大量关注。Raw等[7]基于格点型有限体积法(CV-FVM)研究了均质材料的Fourier导热问题,将该方法成功应用于温度场求解中。笔者等[8]研究了非均质材料的弹性问题,结果表明CV-FVM能够有效避免FEM中出现的应力不连续现象。刘琦等[9-10]基于CV-FVM求解二维不可压材料的线弹性问题和二维复合材料的广义热弹性问题,进一步拓展了CV-FVM的应用范围。
引入高阶网格单元是提高CV-FVM计算精度的有效方法。Charoensuk等[11-12]采用六节点三角形单元(T6)发展二维CV-FVM,用于求解FGMs瞬态热传导问题和热弹性问题,其计算精度高于采用T6单元的FEM。杨国栋等[13]将上述方法应用于滑动轴承的润滑特性分析,结果表明在相同节点数下,采用T6单元的CV-FVM计算结果比采用三节点三角形单元(T3)的CV-FVM的计算结果更加准确。井丽龙[14]采用高阶CV-FVM求解均匀材料板的静力弯曲及自由振动问题,发现采用Q8单元能以更少的节点数计算得到与采用T6单元相当精度的结果。
笔者等利用双线性四边形单元提高了CV-FVM的求解精度[15],并利用交错网格技术发展CV-FVM,有效避免了数值不连续问题[16-17]。在此基础上,本文采用T6单元和Q8单元离散求解域,发展二维高阶CV-FVM用于求解FGMs热弹性问题。通过数值算例验证该方法的正确性,同时分析该方法对于苛刻热环境下FGMs热弹性问题的适用性。
本节建立热应力基本方程及边界条件,研究二维各向同性非均质线弹性材料的稳态热应力问题,其中,控制体Ω的面积为S,控制体的边界为L。
1.1 热传导方程
不考虑热源项,热传导控制方程的积分形式为
(1)
式中:k和T分别是热传导系数及待求解温度。
对于边界上的节点,相应的热传导方程需要考虑恒温边界、热流密度边界和换热边界三种热边界条件:
T=TB
(2)
(3)
(4)
式中:n为控制体边界面的外法线矢量;
TB、qB、hB、T∞分别为恒温边界的边界温度、热流密度边界的热流密度、换热边界的对流换热系数以及环境温度。
1.2 热弹性方程
不考虑体积力,热弹性控制方程的积分形式为
(5)
式中:σ为应力张量,其本构方程和几何方程分别为
σαβ=2Gεαβ+λεαβδαβ-Γ(T-Tr)δαβ
(6)
(7)
式中:σαβ为应力张量σ的分量;
εαβ为应变张量ε的分量;
uα、uβ为位移矢量u的分量;
Tr为参考温度;
Γ为热弹性系数;
G、λ为拉梅常量。G、λ和Γ的值可以根据杨氏模量E和泊松比μ计算得到:
(8)
在平面应变问题中,
(9)
在平面应力问题中,
(10)
对于边界上的节点,热弹性方程考虑位移边界及力边界的影响:
uα=uαB
(11)
σαβnβ=σnB
(12)
式中:uαB、σnB分别为位移边界、力边界上给定的位移和法向压力。
对于T6单元,控制体的划分形式参照文献[11]。对于Q8单元,将它划分为四个三角形子单元1-5-8、2-6-5、3-7-6、4-8-7和一个四边形子单元5-6-7-8(见图1(a))。控制体区域由节点所在子单元中心及子单元边中点连接而成,例如节点N的控制体由A-B-C-D-E-F-G-H连接而成(见图1(b))。采用交错网格技术,将待解变量定义于网格节点,并假设其在控制体内分布均匀;
将材料物性参数定义于网格单元中心,并假设其在网格单元内分布均匀。由于围绕节点的控制体需要多个单元参与,故控制体内材料的物性参数分布不均匀,由此将控制体内不均匀分布的材料物性引入离散方程。
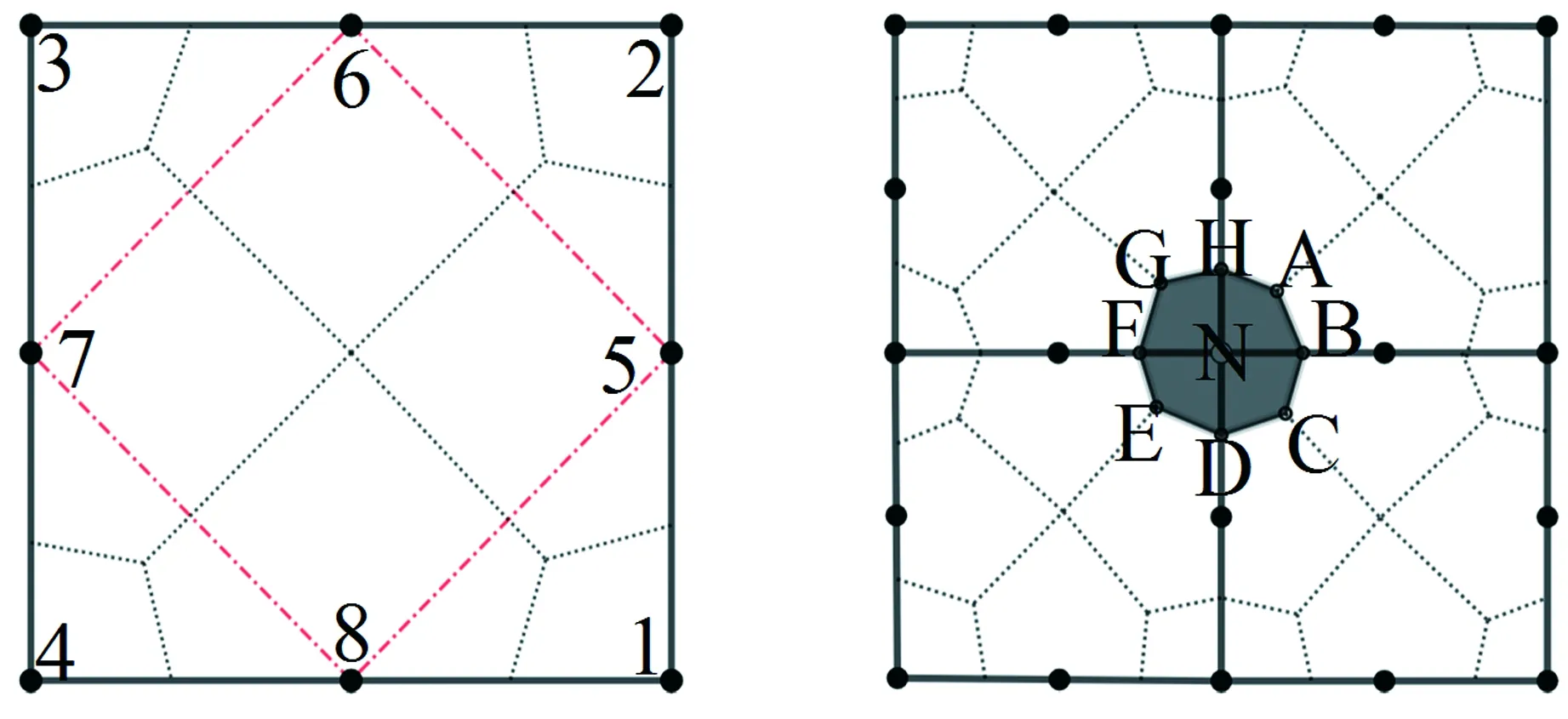
(a) 八节点四边形 (b) 四边形控制体
2.1 热传导方程离散
由高斯公式得
(13)
借鉴FEM的思想,利用形函数对式(13)进行离散:
(14)
式中:下标i代表第i个单元中心,下标ij代表第i个单元内第j个节点;
nc为当前节点相邻单元总数;
ncni为第i个单元上的节点个数;
N为形函数,其导数的积分对于不同网格单元处理方法不同,详细处理过程见2.3节;
Li代表当前节点在第i个相邻单元的控制体边界。
对于边界节点,考虑三类边界的影响:恒温边界、热流密度边界和换热边界。对于恒温边界,温度由式(2)直接给定;
对于热流密度边界及换热边界,将式(3)、式(4)代入式(14)得
(15)
2.2 热弹性方程离散
将本构方程(6)和几何方程(7)代入平衡方程(5)得
(16)
同热传导方程(13),利用高斯公式及形函数可将式(16)离散为
(17)
式中:Liα为积分线Li在α方向上的投影;αi为当前节点第i个相邻单元的热膨胀系数。
热弹性控制方程离散中,对于边界节点同样需考虑边界影响。对于位移边界,位移直接给定为uαβ;
对于力边界,将式(12)带入式(17),则方程最终等效为
(18)
式中:nN为与当前节点相邻的位于力边界上的边界个数;
Liβ为积分线Li在β方向上的投影。
2.3 形函数处理
上述离散方程中涉及到形函数的导数积分,此处给出Q8单元的形函数及其导数积分的处理方法。以积分点1为例,由于形函数对全局坐标(x、y、z)不存在直接关系式,故通过全局坐标对局部坐标(ξ、η、ζ)的关系,构造复合函数求导得
(19)
式中:∂x/∂ξ、∂x/∂η、∂y/∂ξ、∂y/∂η为全局坐标对局部坐标的导数。
式(19)写成矩阵形式:
(20)
定义全局坐标对局部坐标的导数组成的矩阵为雅可比矩阵J,则
(21)
式(21)中,(xi,yi)为Q8单元的8个节点q1~q8的坐标,8个节点如图2中实心点所示。Q8单元图中13个空心点为相应子单元△q3-q7-q6、△q4-q8-q7、△q1-q5-q8、△q5-q2-q6和□q5-q6-q7-q8的边线中心和面中心,例如P、C、D分别是△q5-q2-q6的中心以及边q2-q6、q2-q5的中点;
12个“×”符号标注的是相应的积分点位置,积分点坐标由中点法则确定。式(21)中Ni为Q8

(a) 全局坐标下Q8单元
单元的第i个节点上的形函数(见式(22)),在局部坐标下其偏导数由式(23)给出。
(22)
(23)
由此,得形函数在全局坐标下的导数
(24)
则形函数导数积分为
(25)
式中:(Lx)1、(Ly)1、(Lx)2、(Ly)2分别为节点1周围控制体边界L1、L2在x、y方向上的投影长度。
3.1 热传导问题
下面以FGMs单位方板的热传导问题[18]为例来验证本文提出的高阶CV-FVM处理该类问题的正确性。如图3所示,方板右边界的温度为200 ℃,其余三面的温度为100 ℃,方板为非均质材料,导热系数k(x)按0.5e5xW/(m·℃)变化。
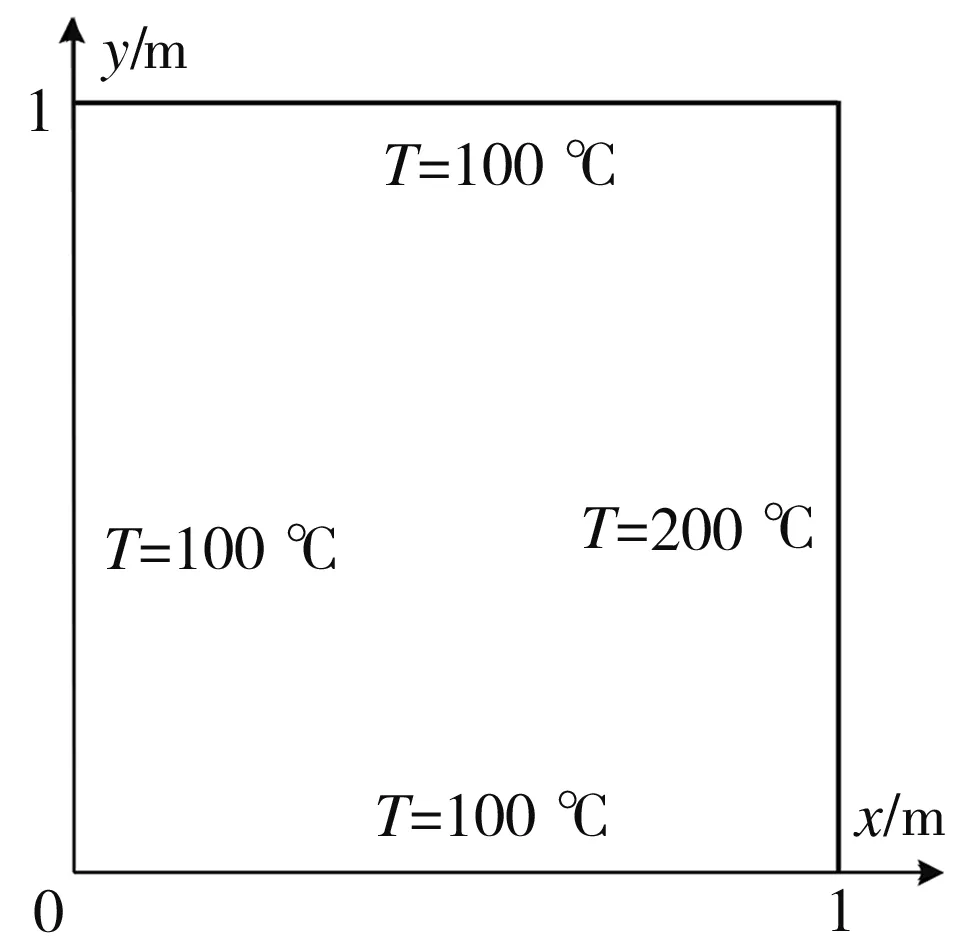
图3 FGMs方形板
方板沿y方向的温度分布计算结果如图4(a)所示,其中低阶CV-FVM采用25×25个Q4网格划分计算域,而高阶CV-FVM仅采用13×13个Q8网格划分计算域。由图4(a)可以看到,CV-FVM求解结果与文献[18]中的理论解吻合良好,即本文方法以较少的网格数就能获得正确的计算结果。

(a) CV-FVM求解结果与理论值对比
为了进一步讨论高阶CV-FVM对苛刻热环境下FGMs热传导问题的适用性,将本文方法的计算结果与不同网格数下FEM计算结果进行对比,见图4(b)。单位方板右上角和右下角存在较大的温度梯度,当网格数较少时,FEM计算结果在右边界附近产生了数值振荡,而高阶CV-FVM计算结果平滑分布。尽管FEM能够通过细密的网格消除数值振荡,但在边界角点处仍存在数值平均的现象,无法严格满足边界给定温度。
3.2 弹性力学问题
为验证本文高阶CV-FVM求解应力问题的正确性,计算如图5(a)所示矩形板的应力[19],并与文献[19]进行结果对比。矩形板由Al和SiC均匀复合而成,泊松比μ取常数0.25,杨氏模量E按式(26)沿y方向变化。
(26)
式中:Al的杨氏模量EAl=70 GPa;
SiC的杨氏模量ESiC=427 GPa。
矩形板的长度L=0.1 m,宽度H=0.04 m,其几何模型及网格模型如图5所示。矩形板左右表面简支,上表面自由,下表面施加向上的正弦载荷p(x),采用平面应变假设。分别基于80和160个T6单元(见图5网格a、b)及80个Q8单元(见图5网格c)划分求解域。图6为不同网格划分下矩形板沿y=0.02 m方向的应力曲线。
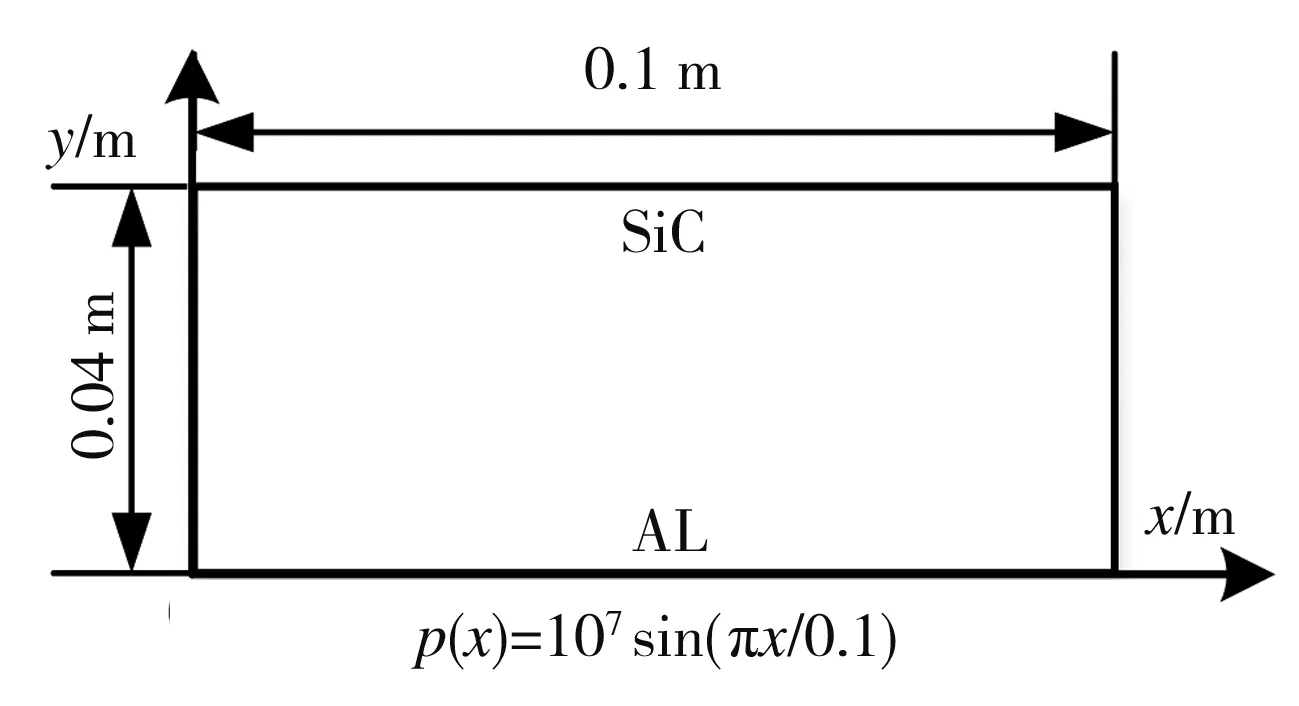
(a) 边界设置
由图6可见,采用3种网格得到的计算结果与文献[19]中理论解吻合较好,验证了本文方法求解FGMs弹性力学问题的正确性;
同时,在相同网格数目下,采用Q8单元得到的结果比采用T6单元得到的结果更准确,计算误差见表1。

图6 矩形板在y=0.02 m处的应力曲线

表1 不同网格类型的平均计算误差
3.3 热弹性问题
为验证本文高阶CV-FVM求解热弹性问题的正确性,计算如图7(a)所示FGMs圆环的热应力场。圆环内表面半径Rin=0.03 m,温度Tin=0 K;
圆环外表面半径Rout=0.09 m,温度Tout=500 K。泊松比μ取常数0.336,杨氏模量E、热膨胀系数α、导热系数k的分布按式(27)沿径向变化。
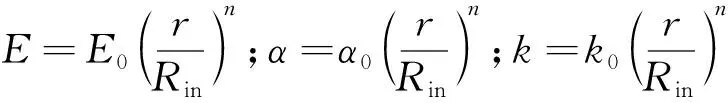
(27)
式中:E0=460 GPa;
α0=7.4×10-6K-1;
k0=20 W/(m·K);
n为非均匀材料变化参数,分别取值0和0.4。
FGMs圆环网格模型见图7(b),采用平面应力假设。分别应用高阶FEM[20]和本文提出的高阶CV-FVM进行数值计算,二者均用800个Q8单元划分求解域,然后与文献[21]中的解析方法进行对比。计算结果如图8所示,包括圆环沿径向θ=0°的温度及应力分布曲线。

(a) 几何模型及边界设置 (b) 网格模型

(a) 温度
由图8可见,高阶CV-FVM计算结果与文献[21]中方法得出的理论解吻合良好,验证了本文方法求解热弹性问题的准确性,而高阶FEM的计算结果却出现了不连续现象,见图8(b)放大部分。这是因为,FEM采用均质单元,未将物性参数的空间变化引入离散过程;
本文高阶CV-FVM则采用交错网格技术,在离散过程中自然考虑了物性参数在控制体内的空间分布,避免了热应力场的数值不连续。
本文发展了一种二维热弹性问题的高阶CV-FVM求解方法,采用T6单元和Q8单元离散控制方程,并利用交错网格技术,将物性参数定义于单元中心,将待解变量定义于单元节点。应用该方法求解热弹性问题,与文献中的理论解进行对比,验证了其正确性,然后分析了该方法对功能梯度材料热弹性问题的适用性,得到如下结论:
(1) 对于存在大温度梯度的FGMs热传导问题,FEM需采用细密网格来消除数值振荡现象,而高阶CV-FVM即使采用粗网格依然能提供合理的数值结果,不存在数值振荡问题。
(2) 对于复杂FGMs热弹性问题,由于高阶CV-FVM采用交错网格技术,在离散过程中自然地考虑了物性参数在控制体内的空间分布,有效避免了FEM中热应力场的数值不连续问题。
(3) 在采用相同网格数的条件下,本文建立的高阶CV-FVM比低阶CV-FVM和采用T6单元的高阶CV-FVM的计算精度要高。
猜你喜欢热传导高阶计算结果一类三维逆时热传导问题的数值求解数学物理学报(2022年1期)2022-03-16冬天摸金属为什么比摸木头感觉凉?红蜻蜓·中年级(2021年12期)2021-12-19有限图上高阶Yamabe型方程的非平凡解数学物理学报(2021年1期)2021-03-29高阶各向异性Cahn-Hilliard-Navier-Stokes系统的弱解数学物理学报(2020年6期)2021-01-14具有非线性边界条件的瞬态热传导方程的二择一结果数学物理学报(2020年5期)2020-11-26滚动轴承寿命高阶计算与应用哈尔滨轴承(2020年1期)2020-11-03不等高软横跨横向承力索计算及计算结果判断研究甘肃科技(2020年20期)2020-04-13一类完整Coriolis力作用下的高阶非线性Schrödinger方程的推导数学物理学报(2018年5期)2018-11-16趣味选路小天使·三年级语数英综合(2017年6期)2017-06-07超压测试方法对炸药TNT当量计算结果的影响火炸药学报(2014年3期)2014-03-20本文来源:http://www.zhangdahai.com/shiyongfanwen/qitafanwen/2023/0918/656213.html