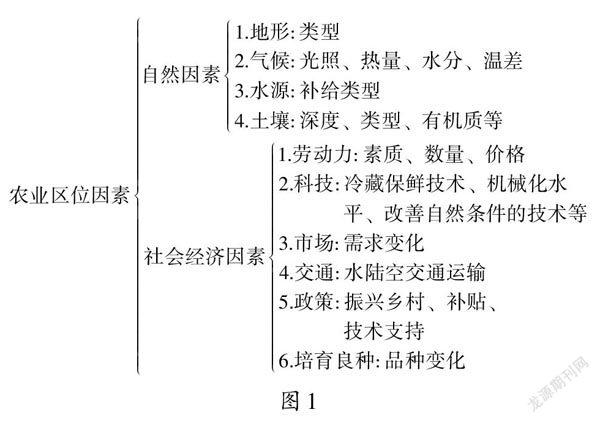
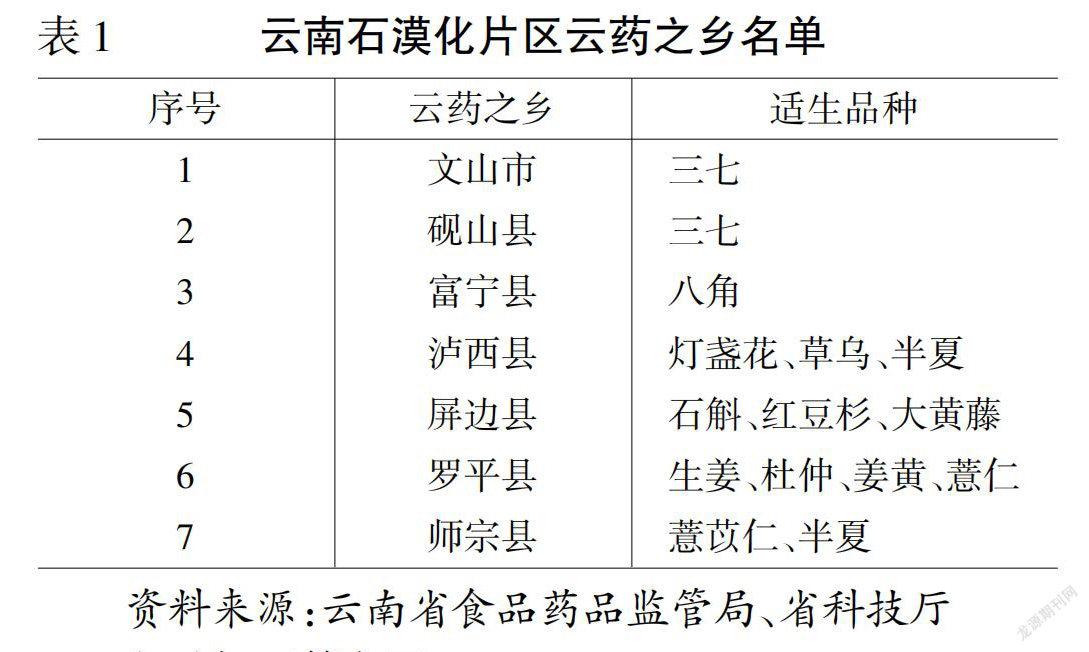
【www.zhangdahai.com--其他范文】
包琪瑶, 韩德广, 刘 锐
(①南开大学数学科学学院,300071,天津市,中国; ②中佛罗里达大学理学院,佛罗里达州,美国)
我们知道作用在Banach空间上的未必完全有界的算子值测度的一般扩张理论[1]可以自然地推广到作用在Banach代数和Banach空间上的有界线性映射,这可以看作是对算子值测度扩张的非交换情形的类比.由Casazza,Han和Larson[2]提出的框架的一般扩张定理指出,即使对于一个Hilbert空间,每一个框架可以有本质上非Hilbert的基扩张,一般情况下其扩张空间必须是Banach空间.这被看作是关于正算子值测度的著名的Naimark扩张理论[3-5]的真正推广.一方面,我们在框架理论和算子值测度的扩张之间建立了一些有趣的联系[1,6-8],另一方面在有界线性映射和von Neumann代数之间也建立了联系.我们知道未必完全有界的任意算子值测度总可以扩张为作用在Banach空间上的幂等的投影值测度. 更一般地,每一个作用在Banach代数上的有界线性映射有一个作用在Banach空间上的有界同态扩张,这里有界线性映射不需要是完全有界的,而且扩张空间通常需要是Banach空间,即使底层空间是Hilbert空间,底层代数是von Neumann代数.因此,任意有界线性映射的有界同态扩张理论真正推广了Stinespring扩张定理[5,9].对于更一般的Banach代数和Banach空间,基于他们的扩张性质可以建立有界线性映射的某种分类理论.代数扩张的扩张空间和扩张范数一般来说不是唯一的.因此,基于扩张空间和扩张范数的有界线性映射的分类涉及到某种结构理论,而在这种结构理论中完全有界映射属于特殊的一类.
本文在第1部分给出作用在一般向量空间上的线性映射的代数同态扩张分类的几个结构性结果.通过介绍典则扩张和万有扩张这两种自然的扩张结构,证明了所有的不可约扩张等价于典则扩张,而且每一个线性极小扩张等价于万有扩张的一个约化扩张.我们通过万有扩张的合成算子的核中的伴随约化子空间给出所有扩张的主要分类结果,并提供一些例子来说明代数扩张理论的复杂性和丰富的结构.第2部分从Stinespring扩张出发,介绍了C*-代数上完全有界线性映射的刻画,并通过一个例子说明即使对交换的纯原子的von Neumann代数也存在没有Hilbert扩张的情况.
1.1 本原和万有扩张
一个线性系统是一个三元组(φ,A,V)使得φ是一个从含幺元代数A到L(V)的保幺元线性映射,其中V是一个向量空间且L(V)表示从V到V的所有线性映射.在A很好理解的情况下,通常从记号中省略.
定义1.1[10]一个线性系统(φ,V)的同态扩张系统是一个从A到线性算子空间L(W)的保幺元同态π(对某向量空间W),且存在一个单射的线性映射T:V→W和一个满射的线性映射S:W→V使得对∀a∈A,如下交换图成立,
即φ(a)=Sπ(a)T,∀a∈A.
我们用(π,S,T,W)来表示这个同态扩张系统,W的维数称为同态扩张系统(π,S,T,W)的扩张维数.称T为扩张系统的分解算子,S为合成算子.如果ker(S)包含一个非零的π-不变子空间,则称(π,S,T,W)是可约的,否则称它为不可约的.

定义1.2[10]一个线性系统(φ,V)的同态扩张系统(π,S,T,W)称为线性极小的,如果span{π(A)TV}=W.如果它既是线性极小的又是不可约的,则称为一个本原扩张.
令(π,S,T,W)为一个同态扩张系统.通过以span{π(A)TV}代替W,则得到一个线性极小扩张.在下面的内容中我们只关注线性极小扩张.
下面给出典则扩张[1]和万有扩张[10]的构造,它们对扩张的结构理论至关重要.
令(φ,A,V)为一个线性系统.对于a∈A,x∈V,由αa,x(·):=φ(·a)x定义αa,x∈L(A,V).令
W:=span{αa,x:a∈A,x∈V}⊂L(A,V).
由πc(a)(αb,x):=αab,x定义πc:A→L(W),则πc是一个保幺元同态.对x∈V,由Tx:=αI,x=φ(·I)x=φ(·)x定义T:V→L(A,V).通过令S(αa,x):=φ(a)x且线性延拓到W,定义S:W→W.如果a∈A,x∈V是任意的,则有
Sπc(a)Tx=Sπc(a)αI,x=Sαa,x=φ(a)x,
因此对∀a∈A,有φ(a)=Sπc(a)T.因此(πc,S,T,W)是(φ,V)的一个同态扩张,称它为(φ,V)的典则扩张.
命题1.3[10]一个线性系统(φ,A,V)的典则扩张是一个本原扩张.
注意到对于一个有限维系统(φ,A,V)的任意线性极小扩张(π,S,T,W),总有
dimW≤(dim A)(dimV).
下面给出一个有极大扩张维数(dim A)(dimV)的线性极小扩张的构造.
令W=A ⊗V.定义πu:A→L(W),T:V→W和S:W→V分别由

Tx=I⊗x,
给出,那么πu是一个同态且对∀x∈V和∀a∈A,有
Sπu(a)Tx=Sπu(a)(I⊗x)=S(a⊗x)=φ(a)x,
因此(πu,S,T,W)是(φ,V)的一个同态扩张系统.另外,由于πu(a)Tx=a⊗x,有
span{πu(a)Tx:a∈A,x∈V}=W,
因此(πu,S,T,W)是一个线性极小扩张系统且具有性质dimW=(dim A)(dimV).
定义1.4[10]以上构造的扩张(πu,S,T,W)称为(φ,V)的万有扩张.
1.2 结构定理
在这一部分给出关于所有线性极小同态扩张分类的主要结果.
定义1.5[10]令(π1,S1,T1,W1)和(π2,S2,T2,W2)为线性系统(φ,V)的两个线性极小同态扩张系统.如果存在一个双射的线性映射R:W1→W2使得RT1=T2,S2R=S1且π1(a)=R-1π2(a)R对∀a∈A,则称这两个同态扩张系统是等价的.
以下定理说明所有的本原同态扩张系统是等价的.
定理1.6[10]如果(π1,S1,T1,W1)和(π2,S2,T2,W2)是(φ,A,V)的两个本原同态扩张系统,那么(π1,S1,T1,W1)和(π2,S2,T2,W2)是等价的.
下面的定理说明万有扩张实际上是“最大的”扩张系统.
定理1.7[10]一个线性系统(φ,V)的任意线性极小同态扩张等价于它的万有扩张的一个约化同态扩张系统.
为了对线性极小同态扩张系统进行分类介绍以下定义.
定义1.8[10]对于一个线性系统(φ,V),令(πu,S,T,W)为万有扩张系统且(π1,S1,T1,W1)为一个线性极小同态扩张系统,称πu-不变子空间
为伴随于(π1,S1,T1,W1)的约化子空间.
对于一个给出的线性系统,以下定理给出了它的所有线性极小同态扩张系统的分类.
定理1.9[10]令K1和K2分别为伴随于极小同态扩张系统(π1,S1,T1,W1)和(π2,S2,T2,W2)的约化子空间.那么这两个同态扩张系统是等价的当且仅当K1=K2.


后面的例子表明即使是在有限维的情形(即dimV<∞,dim A<∞)也会存在无穷多不等价的线性极小同态扩张系统.
我们给出一个与扩张理论相关的较弱版本的等价[10]:如果(π1,S1,T1,W1)为线性系统(φ,V)的线性极小扩张系统,π2是从A到L(W2)的一个同态使得π1和π2在通常意义下是等价的,即π1(a)=R-1π2(a)R(∀a∈A)对某同态R:W1→W2,那么 (π2,S2,T2,W2)是一个等价的扩张系统且S2=S1R-1,T2=RT1.
下面介绍约化不变子空间的等价概念,给出线性极小同态扩张系统的同态π1和π2等价的条件.
定义1.10[10]令(πu,S,T,W)为线性系统(φ,V)的万有扩张系统. ker(S)的两个πu-不变子空间K1和K2称为强同构的,如果存在一个同构R:W→W使得R(K1)=K2,且对 ∀a∈A和∀w∈W,πu(a)Rw-Rπu(a)w∈K2,即对∀a∈Aπu(a)的商映射和R在W/K2上可交换.
定理1.11[10]令K1和K2分别为线性极小同态扩张系统(π1,S1,T1,W1)和(π2,S2,T2,W2)的约化子空间,那么π1和π2是等价的当且仅当K1和K2是强同构的.
证明由定理1.7,可以假设(πi,Si,Ti,Wi)是伴随于Ki(i=1,2)的万有扩张的约化同态扩张.

类似地,有


定理1.9和定理1.11给出了线性极小同态扩张的两种分类,基于由S(a⊗x)=φ(a)定义的映射S:A⊗V→V的核中的万有扩张不变子空间.下面通过构造一些具体的例子来说明代数扩张理论的复杂性和丰富的结构.
令
那么M是包含在ker(S)中的最大的πu-不变子空间.因此,由定理1.6可知万有同态扩张等价于本原扩张当且仅当M={0}.另外可得以下结论.
命题1.12[10]一个线性系统(φ,V)只有线性极小同态扩张的一个等价类当且仅当M={0}.
推论1.13[10]令(φ,A,V)为一个线性系统.如果ker(φ)包含一个真左理想,那么万有扩张不等价于它的本原扩张.
推论1.14[10]令(φ,A,V)为一个线性系统使得dim(V)=1,那么它的万有扩张和本原扩张是等价的当且仅当ker(φ)不包含任意真左理想.





为了确定同态扩张的其余等价类,首先需要确定ker(Su)中的所有πu-不变子空间.注意到 ker(Su)=span{e2,e4,e5},易证其极大πu-不变子空间是span{e2,e4},且span{e2,e4}的任意一维子空间也是πu-不变的.因此,由定理1.9可知4维同态扩张系统只有一个等价类,5维同态扩张系统有无穷多不等价类.
同态扩张系统的4维等价类由(π4,S4,T4,4)表示,由如下给出
伴随于πu-不变子空间K1=span{e2}和K2=span{e4}的两类同态扩张系统分别由(π5,1,S5,1,T5,1,5)和(π5,2,S5,2,T5,2,5)表示,由如下给出

对于三角矩阵的转置映射,情况大不相同.下面给出在T2和T3上转置映射的情况.
例1.16[10](ⅰ)令τ:T2→2为转置映射.那么万有扩张系统由

典则扩张系统由

另外,有ker(Su)=span{e2-e6,e3,e4,e5}.
在ker(Su)中,极大πu-不变子空间是M=span{e4,e5},且对任意给出的α,β,一维子空间Kα,β=span{αe4+βe5}是πu-不变子空间,所以再次表明存在5维扩张的无穷多不等价类.对应于K1,0和K0,1的2个特殊情形表示如下,


(ⅱ)令τ:T3→3为转置映射,则那么典则扩张πc:T3→10由

对于一般矩阵的转置映射,情况如下.
例1.17令τ:2→2为转置映射,则那么万有扩张系统表示如下,

因此,ker(Su)=span{e1-e4,e2,e3,e6,e7,e5-e8}.
由于ker(Su)中没有非平凡πu-不变子空间,故以上公式也给出了典则扩张.
例1.18[10]令v:2→2为线性映射
那么有(线性极小)扩张π:2→4由



2.1 Hilbert扩张
用B(H)表示 Hilbert空间H上所有有界线性算子构成的代数.
用Mn(A)表示n×n矩阵的集合,其元素来自A.Mn(A)的元素由(ai,j)表示.
令A和B为两个C*-代数,φ:A→B为一个线性映射,通过φn((ai,j))=(φ(ai,j)),定义φn:Mn(A)→Mn(B).
映射φ称为正的,如果φ把A中的正元素映为B中的正元素.
映射φ称为完全正的,如果对所有的自然数n,φn是正的.


首先给出几个经典的扩张定理.
定理2.2[5](Sz.-Nagy扩张定理) 令T为Hilbert空间H上的一个收缩算子,那么存在一个包含H作
为一个子空间的 Hilbert 空间K和K上的一个酉算子U使得Tn=PHUn|H.
定理2.3[5](Naimark定理) 令E为X上一个正则的,正的,B(H)-值测度,那么存在一个Hilbert空间K,一个有界线性算子V:H→K和X上的一个正则的,自伴的,谱的,B(K)-值测度F使得E(B)=V*F(B)V.
定理2.4[5](Stinespring扩张定理) 令A为一个含幺元C*-代数,令H为一个Hilbert空间,令φ:A→B(H)为一个完全正映射,那么存在一个Hilbert空间K,一个含幺元*-同态π:A→B(K)和一个有界算子V:H→K,且‖φ(1)‖=‖V‖2使得φ(a)=V*π(a)V.
很容易证明任意具有形式φ(a)=V*π(a)V的映射是完全正的.因此,Stinespring扩张定理刻画了从任意C*-代数到任意Hilbert空间中有界线性算子的代数上的完全正映射.下面从Stinespring扩张出发,给出完全有界线性映射的刻画.


由于M2(A)包含M2的复制,Hilbert空间K1可以用这样的方式分解为K1=K ⊕K,*-同态π1:M2(A)→B(K ⊕K)具有形式
其中π:A→B(K)是一个含幺元*-同态.因此,有V:H ⊕H→K ⊕K是一个等距,且
对∀h∈H,有

证毕.
对于任意有界线性映射的有界同态扩张理论真正推广了Stinesping扩张定理,阐明了C*-代数上一个有界线性映射有一个*-同态扩张(作用在一个Hilbert空间上)当且仅当它是完全有界的.
2.2 非Hilbert的扩张
称一个映射是正规连续的,即超弱,或σ-弱,或w*连续的.
定义2.6[2]Banach空间X上的一个无条件框架是一个序列对{xi,yi}i∈,其中xi∈X,yi∈X*(X的对偶空间),满足对∀x∈X,且这个级数无条件收敛.
定理2.7[1]令H为一个可分的Hilbert空间,令{xi,yi}为H的一个无条件框架,那么由

定义的从l∞到B(H)的映射φ是良定义的、含幺元的、线性的且超弱连续的.
下面通过一个例子说明即使对交换的纯原子的von Neumann代数也存在没有Hilbert扩张的情况.这个例子表明对于一个Hilbert空间存在一个无条件框架,它诱导的算子值测度没有Hilbert空间扩张.等价地,它不能通过重调来得到一个有Hilbert空间扩张的无条件框架.这个构造基于Osaka[11]的一个从l∞到B(H)的正规的非完全有界映射的例子.
定理2.8[1]对于一个Hilbert空间,存在一个无条件框架使得它诱导的算子值测度不是完全有界的,因此它不能通过重调来得到一个有Hilbert空间扩张的无条件框架.
由于如果一个无条件框架有一个Hilbert空间扩张,那么它诱导的算子值映射是完全有界的,且重调无条件框架诱导相同的算子值映射,因此,只需要表明对于Hilbert空间存在一个无条件框架使得它诱导的算子值测度不是完全有界的.首先需要以下引理.
引理2.9[1]令{An}为Hilbert空间H上一个有限秩有界线性算子序列使得
(ⅰ)AnAm=AmAn=0对所有n≠m;
(ⅱ)存在相互正交的投影{Pn}使得An=PnAnPn对所有n;



下面证明定理2.8.