【www.zhangdahai.com--其他范文】
张 森 张 江 曹南斌
(河北地质大学数理教学部 河北 石家庄 050031)
在大学物理实验中,最普遍的等厚干涉实验是牛顿环实验.最早的牛顿环实验是1675年牛顿在制作天文望远镜时,偶然发现将一个望远镜的物镜放在平板玻璃上,就可以实现光学中常见的定域等厚干涉现象.牛顿环在大学物理实验数据误差处理教学中起着重要作用,更精确的牛顿环估计方法将提高学生对等厚干涉和误差统计分析领域的理解[1-2].
牛顿环实验基本方法是通过读数显微镜对牛顿环的干涉条纹进行测量,进而计算出平凸镜的曲率半径.为了提高曲率半径的测量精度,人们从各方面进行了详细研究.计算机软件在误差统计分析数值处理中起到了决定性作用[3].在压力的作用下,平凸镜在接触面附近发生了不可避免的弹性形变,使得暗斑“吞噬”了若干条明暗圆环,因此,实验只能精确测出暗环的直径,却很难确定暗纹的误差不确定度.所以,既然误差不可避免,我们将注意力转移到如何构建更准确的统计模型,并进一步得到测量数据的最佳估计值,从而提高计算曲率半径的精度.同时,建立牛顿环测量数据不确定误差参数统计模型对于牛顿环在测量薄膜、玻璃弹性模量、液体折射率等方面应用也具有重要意义.
在过去几十年,高等院校大学物理实验主要使用两种不同的实验方法分析牛顿环实验数据:逐差法和最小二乘法.逐差法一般采用的方法是把测量的偶数个数据对半分成前后两组,后一组的数据与前一组的对应数据逐差再取平均.最小二乘法是统计学中最常见的回归分析方法.最近十几年,众多物理实验对测量不确定度分析要求越来越高,这对大学物理实验教学研究起到了极大促进作用.然而,不同方法测定的牛顿环平凸透镜的曲率半径有一定的差异,这是多年以来存在于实验教学领域尚需讨论的疑难问题[4-5].如果实验数据存在特殊的离群点,那就需要选择更稳健的误差统计分析方法.
不同大学物理实验方法测量结果之间的偏差是长期困扰广大师生的难题.为此不同学派的理论学家提出了多种不确定度统计模型解释.对于稳健性统计模型,我们已经基于实验数据集,将MFV统计方法(most frequent value),应用到观测数据最佳估计值问题[6-7].在我们之前的工作显示,误差分布完全可能是非高斯的,且测量数据之间可能存在无法精确衡量的相关性.
加权平均方法也是一种常见误差处理统计方法.应用加权平均方法要满足一些假设,包括数据在统计意义下独立分布和随机误差满足高斯分布.然而实验测量的误差分布可能是非高斯的,采用加权平均方法不一定能够得到合理的中心估计和不确定度置信区间.中位数方法具有对异常值不敏感特性,已经有很多应用中位数统计处理实验数据集的工作[8].
在非高斯分布情况下,传统方法的应用受到了巨大限制.为详细分析测量过程中的统计误差和系统误差,许多研究人员选取误差参数模型分析物理测量数据.文献[9]在2020年应用贝叶斯分层模型,计算出实验数据的拟合值.文献[10]应用频率学派方法构造了一种具有优良稳健性的模型,该模型对数据误差的建模分析较为全面.
本文将详细分析Cowan的统计方法,以及频率学派不确定误差参数统计模型的构造和计算过程.基于河北地质大学物理实验协会学生测量的牛顿环6~15级实验数据结果,如表1所示,重新构建其不确定误差参数统计模型,以减小异常值的影响.最后给出数值计算拟合结果.
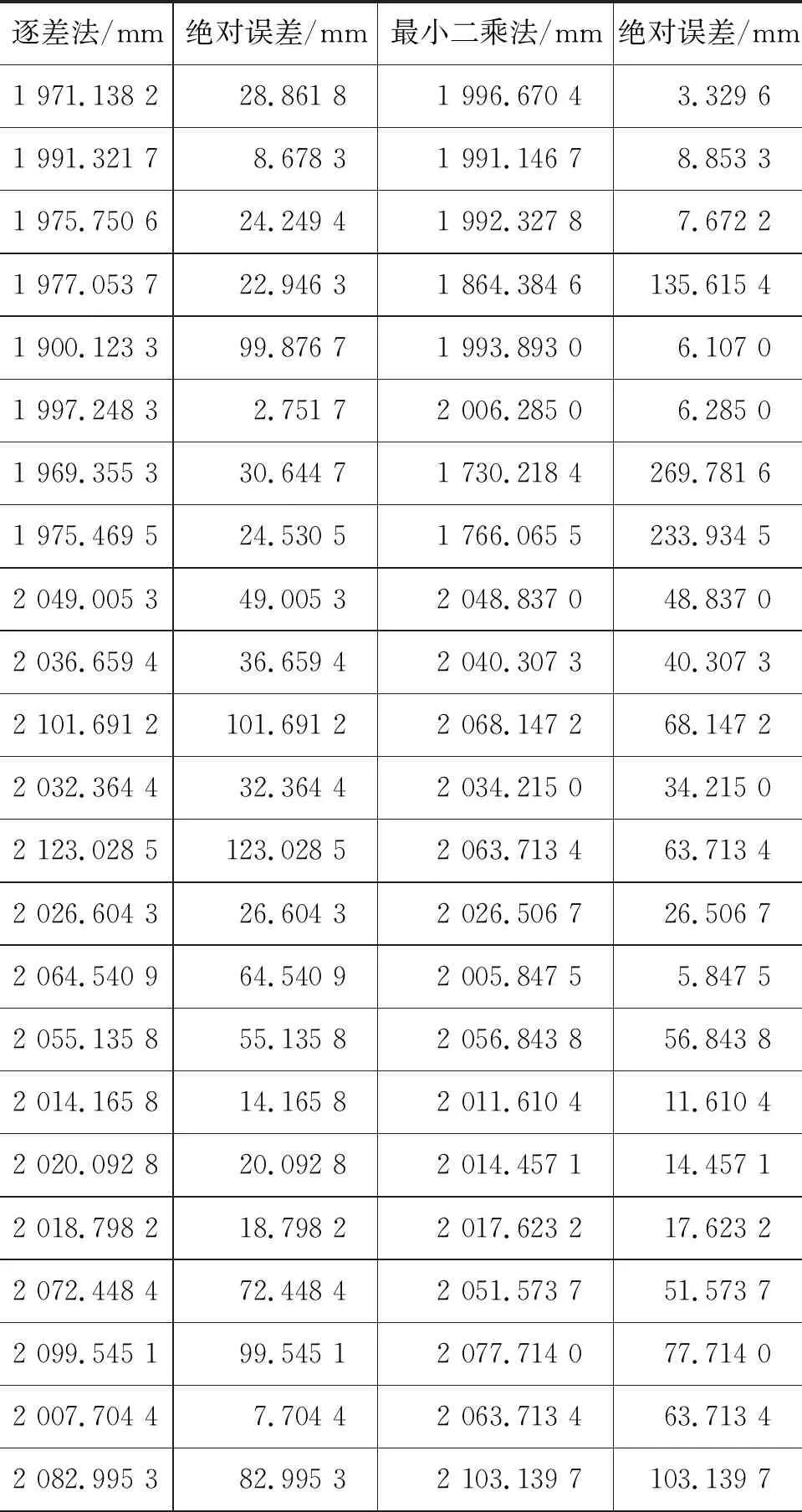
表1 牛顿环实验曲率半径数据结果

续表1
2.1 参数估计和置信区间
频率学派参数估计常用方法为极大似然估计和最小二乘法.这两种方法的应用均需满足一定的假设,特别是在应用极大似然估计时,需要预先假设数据的分布.通过引入额外的冗余参数,可以降低可能出现的错误先验信息影响,从而提升模型的稳健性,但这可能会使得模型的计算更为复杂.
基于频率学派对概率的定义,频率学派置信区间边界由测量数据的函数给出.其定义为:覆盖概率指一个集合中包含参数真实值的概率.构造置信区间使覆盖概率大于给定的置信度.观测值Y的概率密度函数为p(y|θ),其中θ是未知参数.对参数θ和置信度1-α,有y1(θ,α)与y2(θ,α),满足

(1)
通常y1(θ,α)与y2(θ,α)是单射,因此在给定的置信度下,可以求出反函数θ1(y)和θ2(y).假设y0与θ0分别为物理量真值和参数真值.则θ0落在[θ1,θ2]当且仅当y0落在[y1(θ0),y2(θ0)],对于所有的θ0值均成立.因此
1-α=P[y1(θ) (2) 这就是置信区间的Neyman构造方法.置信区间构造方法并不唯一,常见选取置信区间方法为:选取中心对称区间、单侧区间,或构造似然比统计量进行检验求解.另外,若观测值服从离散分布,置信区间的覆盖概率可能大于1-α. 频率学派置信区间的构造方法与假设参数真值为θ0,并对其进行假设检验是等价的.常用的一种检验为似然比统计量检验,似然比λ定义为 (3) (4) 置信区间的数值计算有时会很困难,可以通过蒙特卡罗(MC)方法求解.如果模型中使用似然函数较为复杂,那么运算过程中将包含较多难算的最优化问题. 对于构造似然比时引入冗余参数,Cowan提出一种应用轮廓似然比(profile likelihood ratio)统计量的不确定误差参数统计模型.此模型对数据误差应用Gamma分布进行建模,通过调整超参数r,得到具有优良稳健性的拟合结果.轮廓似然比定义为 (5) 图1展示了正态分布样本的轮廓似然直方图与χ2分布的对比.红色直线代表标准的χ2分布PDF,样本轮廓似然比的MC模拟结果在归一化后显示为蓝色直方图.在满足一定假设的前提下,-2lnλ服从χ2分布.然而若某些假设条件不成立,比如参数间有着相关性的条件下,-2lnλ则并不总是服从χ2分布. 图1 特定参数下-2ln λ的分布 对于牛顿环实验数据统计分析问题,可以选取高斯分布的似然函数,而对误差应用Gamma分布模型进行刻画.通过超参数控制误差波动,可以在实验数据集上得到较好的拟合效果.高斯分布通常被认为是在许多未知影响因素相互叠加时的近似分布,这里为p(y|μ,θ)选取高斯分布的似然函数是合理的.可以构造如下似然函数 (6) 这代表假设观测数据y服从一个高斯分布,其参数为μ,θ.θ的估计值为u,假设其服从高斯分布,即 (7) (8) (9) (10) (11) 调整超参数r的值,可以控制模型对于异常值的敏感性. 在对模型参数进行化简后,对数似然函数为 (12) 图2 模型在一组实验数据上的拟合结果 计算所得的牛顿环测量数据估计值及其置信区间如图3所示.图中曲线代表负对数似然作为参数μ的函数,根据Wilks定理,使得-2lnλ从最小值增大1时的μ值即为其68.3%置信区间的边界,在图中以竖直虚线显示.不同的子图显示了不同参数设置下的拟合结果.计算得到,选取r=0.2时,牛顿环测量数据估计值为R=1 998.79,对应的置信区间边界为[1 990.34,2 007.32].当r=0.4时的置信区间总长略大于r=0.2时的结果,这与之前的模型分析吻合. 图3 模型计算结果 此外,模型对采用逐差法的数据拟合结果为R=1 998.25-9.71/+9.47,对最小二乘法的数据结果为R=1 998.97-7.47/+7.90.在计算过程中,当r=0.6时,-2lnλ的函数曲线有更多的起伏,这表示当r过大,模型的预测效果可信度较低.因此,我们选取参数值r=0.2作为最优参数值. 图4对比了牛顿环实验测量数据和不同统计模型计算结果,图中阴影部分为不确定误差参数模型计算所得的置信区间.在垂直虚线左侧为随牛顿环实验变化的测量数据列,右侧为模型拟合结果,包括加权均值、中位数以及本文得到的结果.图4下方子图展示了以误差统计模型为基准进行归一化之后的结果. 此误差统计模型的重要特性之一是,随着参数值的增加,拟合数据的值对显著偏离中心值的游离点(异常值)变得不那么敏感.图4中体现出了这种特性,结合在实验数据上的拟合效果,最终我们选取参数值r=0.2.此时的不确定误差参数统计模型相比起中位数结果更接近于数据整体的加权均值,且对数据有着较好的覆盖率. 图4 原始数据分布及模型预测结果对比(下方子图为归一化后的相对误差分布) 总而言之,物理实验的一个主要目标是对一些关键物理量进行精确测量.牛顿环实验数据不同方法间长期存在的偏差是基础光学和大学物理实验数据处理的疑难问题之一.对牛顿环测量误差进行稳健统计建模分析是获取可信估计值及置信区间的关键.本文应用Cowan不确定误差参数统计模型,对牛顿环实验数据使用Gamma分布对误差建模,得到曲率半径估计值为R=1 998.79-8.45/+8.53,计算结果显示出良好的稳健性,并且对异常值的干扰不敏感. George E. P. Box 指出:“所有模型都是错误的,但有些模型是有用的”.每个计算统计模型的一些潜在假设并不一定都严格成立.Gamma误差模型在一定程度上可以克服传统方法不实假设的问题,这也启发我们在类似情况下应用不确定误差参数模型,并进一步研究其他大学物理实验测量数据的不确定度问题.2.2 似然比统计量的构造和应用


2.3 不确定误差参数统计模型