【www.zhangdahai.com--其他范文】
聂晓汤 ,吴爱迪
(1.福建师范大学 数学与统计学院,福建 福州 350117;
2.福建农林大学 计算机与信息学院,福建 福州 350002)
采用亚纯函数唯一性理论中的一些基本记号和结论,如T(r,f),m(r,f),N(r,f)等,参见文献[1].如果亚纯函数α 满足T(r,α)=S(r,f),则称α 为关于f (z)的小函数,其中S(r,f) 表示任意满足S(r,f)=o(T (r,f))(r →∞) 的量,可能除去r 的一个线性测度为有穷的集合.此外,还用到下述定义.
定义1[2]设k 是一个非负整数或∞,a 为复数.定义Ek(a,f)表示f-a 的零点集合,其中,若m≤k,则f-a的m 重零点记m 次;
若m>k,则记k+1 次.如果Ek(a,f)=Ek(a,g),则称f 与g 以权k 分担值a,记作(a,k).特别地,如果f 和g 分担值aIM 当且仅当f 和g 分担(a,0);
如果f 和g 分担值aCM 当且仅当f 和g 分担(a,∞).
定义2令P(z)=amzm+am-1zm-1+…+a1z+a0是非零多项式,其中a0(≠0),a1,…,am-1,am(≠0)均为复常数,m 为正整数.记d=gcd{λ0,λ1,…,λm},这里的
涉及亚纯函数微分多项式分担值的唯一性理论是近年来研究的热门课题,许多学者对该方面进行深入研究并取得了一系列有趣的结果,详见文献[3-5].首先回顾Yang 等[4]所证结果.
定理A[4]设f 和g 为两个非常数亚纯函数,n≥11 为整数.如果fnf ′和gng′分担1CM,则f=c1ecz,g=c2e-cz,其中c,c1,c2是非零常数且满足(c1c2)n+1c2=-1,或者f=tg,其中t 是常数满足tn=1.
近年来,随着Nevanlinna 理论差分模拟[6-7]的兴起,许多学者对复差分多项式的唯一性问题进行深入研究,相应于定理A 的差分问题研究得到一系列有趣的结果[8-11].其中,祁晓光等[8]获得了如下结果.
定理B[8]设f 和g 为两个有穷级超越整函数,n≥6 为正整数,c 为非零复数.如果fnf (z+c) 和gng(z+c) 分担1CM,则fg=t 或者f=tg,其中t 为常数且tn+1=1.
随后,李效敏等在文献[9]中考虑了分担小函数的情况,证明了:若n≥m+6,则fn(fm-1)f(z+c)和gn(gm-1)g(z+c)CM 分担一个小函数时整函数f 和g 满足f=tg,其中t 为常数且tm=1.然而针对亚纯函数的情况,李效敏等[10]于2014 年得到了如下结果.
定理C[10]设f 和g 为两个有穷级超越亚纯函数,c 为非零复数,a(z)是关于f 和g 的非零小函数,n,m为正整数且满足n≥m+12,m≥2.若fn(fm-1)f(z+c)和gn(gm-1)g(z+c)分担a(z),∞CM,f 和g 分担∞IM,则f=tg,其中t 为常数且tm=1.
设c 为非零复数,Δcf,Δkcf 分别指f 的差分算子和k 阶差分算子,易见

引入一个线性差分算子L(z,f),如式(1)所示,它在一定程度上推广了Δcf 和Δkcf.
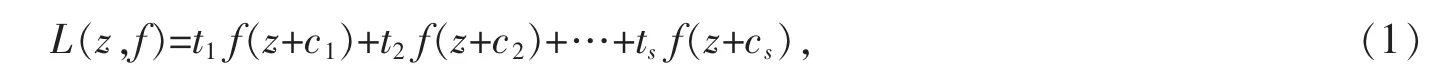
这里c1,c2,…,cs为互不相同的复数,t1,t2,…,ts为不全为零的复常数.记s 为线性差分多项式L(z,f)的项数且s≥1.
结合引入的线性差分算子L(z,f),利用权分担思想获得了如下结果.
定理1设f和g 为有穷级超越亚纯函数,P(z)如定义2 所示,L(z,f)和L(z,g)如式(1)所示,a(z)是关于f和g 的非零小函数.若fnP(f)L(z,f)与gnP(g)L(z,g)分担(a(z),l),f 和g 分担∞IM,其中0≤l<∞,n,m,s 为正整数且下列条件之一成立:

则下列情况之一成立:
1) f=tg,其中t 为常数满足td=1,d 如定义2 所示;
2) f,g 满足代数方程R(f,g)≡0,其中

在定理1 中,若l→∞,则可得下面的推论.
推论1设f 和g 为有穷级超越亚纯函数,P(z)如定义2 所示,L(z,f)和L(z,g)如式(1)所示,a(z)是关于f 和g 的非零小函数.假设fnP(f)L(z,f)与gnP(g)L(z,g)分担a(z)CM,f 和g分担∞IM.若n,m,s 为正整数且满足n>m+6s+7,则下列情况之一成立:
1) f=tg,其中t 为常数满足td=1,d 如定义2 所示;
2) f,g 满足代数方程R(f,g)≡0,其中

注1当L(z,f)的项数s=1 时,推论1 改进了定理C.事实上,当P(z)=zm-1 时,由推论1 的结论2 可知:fn(fm-1)f(z+c1)=gn(gm-1)g(z+c1),取A=fg,则有(An+mA(z+c1)-1)gm=AnA(z+c1)-1.若An+mA(z+c1)-1=0,则Am=1,此时A 一定是常数,故有f=tg,tm=1.若An+mA(z+c1)-1≢0,对An+mA(z+c1)运用第二基本定理可推得矛盾.
为了证明方便,首先引入一些引理和符号.
设f 和g 为两个非常数亚纯函数且a 为复数,Np(r,a;
f)表示f-a 的零点计数函数,其中重数m<p,计m 次;
m≥p,计p 次.
引理1[1]设f 为开平面上非常数亚纯函数,an(≠0),an-1,…,a1,a0均为f 的小函数,则T(r,anfn+an-1fn-1+…+a1f +a0)=nT(r,f )+S(r,f ).
引理2[7]设f 为有穷级非常数亚纯函数,c 为非零有穷复数,则

引理3[7]设f 为有穷级非常数亚纯函数,c 为非零有穷复数,则

引理4[12-13]设f 和g 是两个非常数亚纯函数.如果f 和g 分担(1,l)和(∞,0),其中l 为非负整数.设若H≢0,则
i) 当2≤l<∞时,

ii) 当l=1 时,
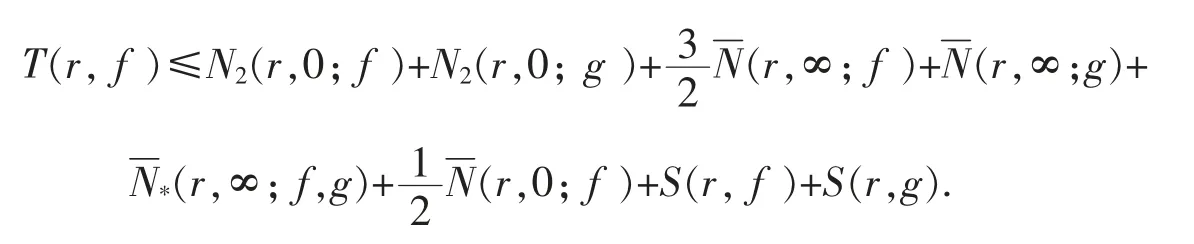
iii) 当l=0 时,

置

由于F 和G 分担(a(z),l),若不考虑a(z)的零点和极点,F1与G1分担(1,l),且
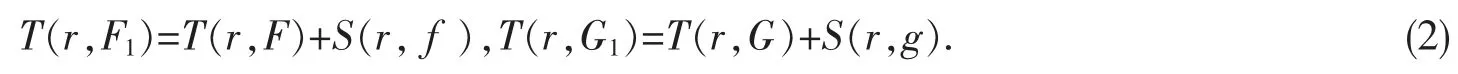
根据引理1 和引理3 可知
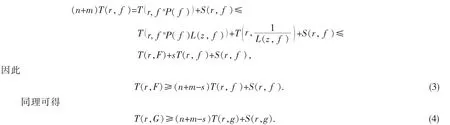
另一方面,对F 运用第二基本定理可得
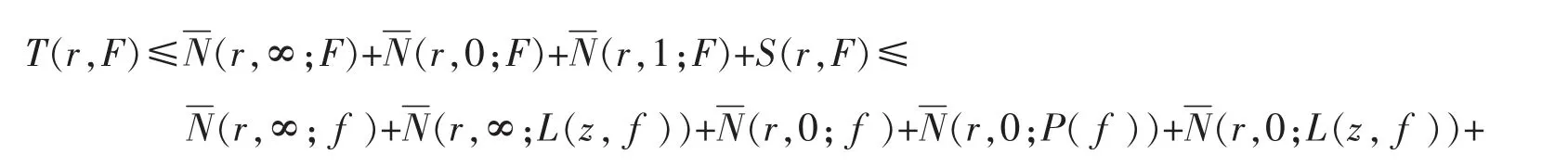
再由式(3)可得
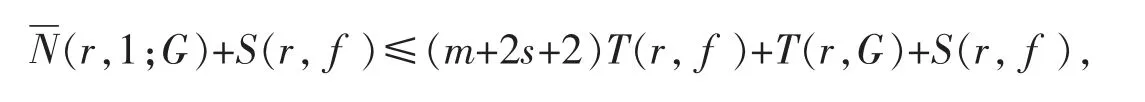
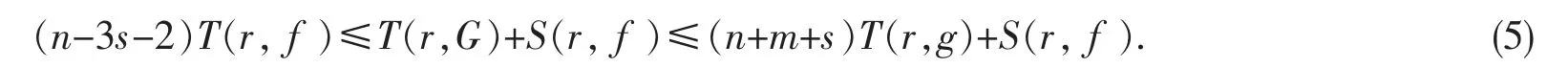
对G 运用上述相同方法可得

由式(5)和式(6),有
因此,为了方便,不妨记

由引理1 和引理3 可知
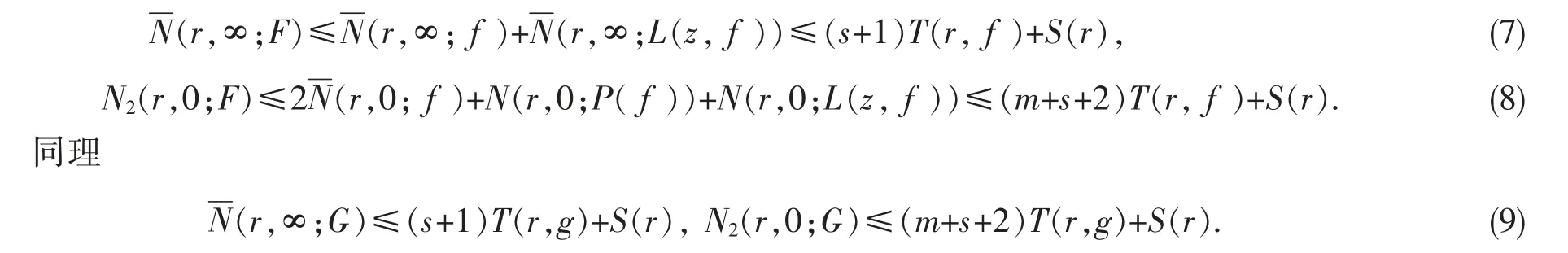
下面分两种情况讨论.
情况1若H≢0,考虑下列三种情况.
子情况1.1当2≤l<∞时.由引理4,有
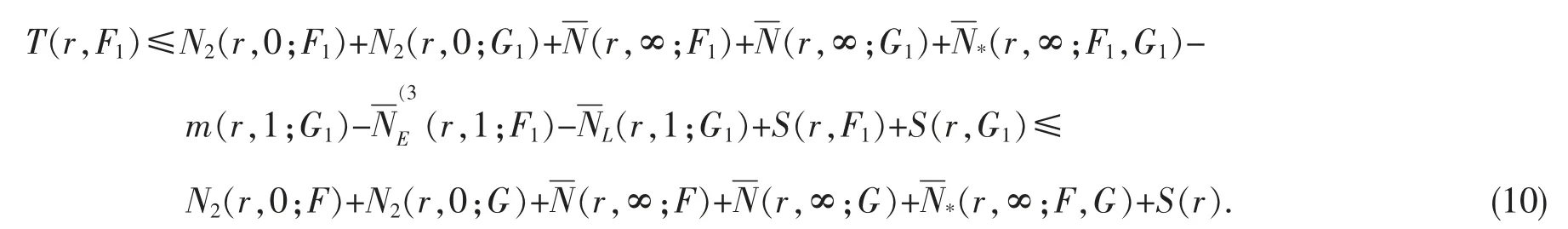
注意到

由式(7~11)可得
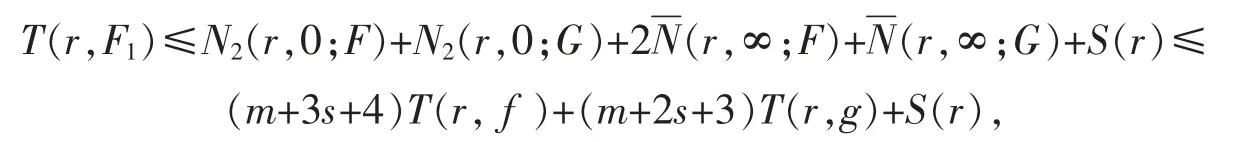
进一步地,由式(2)和式(3)可知

同样地,有
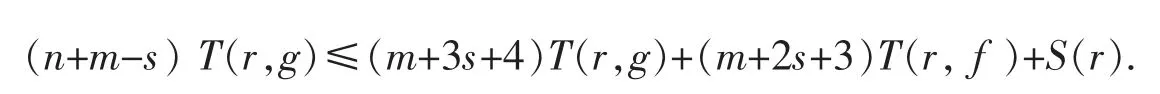
将以上两式相加可得

这与假设条件n>m+6s+7 矛盾.
子情况1.2当l=1 时,由引理1 和引理3,有

根据式(7~9),式(11~12)和引理4 可得


结合式(2)和式(3)可推导得

将上述两式相加可得

子情况1.3当l=0 时,由引理1 和引理3,有

根据式(7~9),式(11~13)和引理4 可得

进一步地,由式(2)和式(3)可知

同理
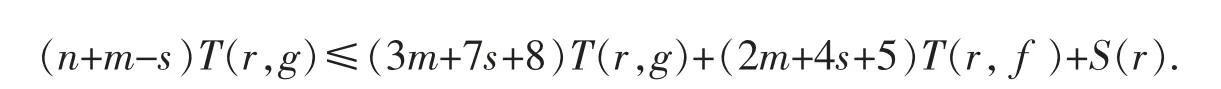
结合以上两式可得
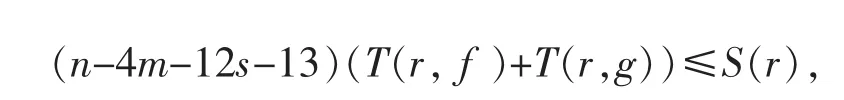
与n>4m+12s+13 矛盾.
情况2H≡0,即,连续积分两次可得

其中A(≠0)和B 为常数.
1) B≠0 且A≠B,若B=-1,由式(14),有F1=.根据式(7),式(9),式(13)和第二基本定理可得

进一步地,根据式(2),式(4),式(5)可推导得
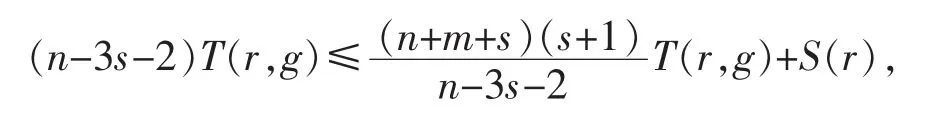
与假设条件矛盾.
2) B≠0 且A=B,若B≠-1,类似1)的讨论可得矛盾.若B=-1,由式(14)可得F1G1=1,即
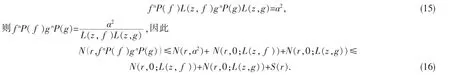
另一方面,由引理2 可知

由式(16~18)及f 和g 分担∞IM,可知

进一步地,利用第二基本定理可得
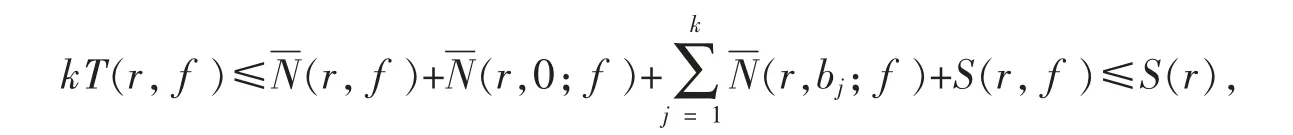
其中bj(j=1,2,…,k)是方程P(z)=0 的根,这是不可能的.
3) B=0,若A≠1,则G1=AF1-(A-1),类似1)的讨论可得矛盾,因此A=1,也就是F1=G1,即



因为am≠0,g 为有穷级超越亚纯函数,若hn+m+1-1≠0,根据式(22)和引理1 可知T(r,g)=S(r),矛盾,因此hn+m+1=1.若am-1≠0,假设hn+m-1≠0,同样地,由式(22)和引理1 可推得hn+m=1.以此类推,可得hd=1,d=gcd {λ0,λ1,…,λm},其中

故有f=tg,t 为常数且满足td=1,d 如上所示.
若h 不是常数,则由式(20)可知,f 和g 满足代数方程R(f,g)≡0,其中R(w1,w2)=w1nP(w1)L(z,w1)-w2nP(w2)L(z,w2).至此,定理1 证明完毕.
猜你喜欢 正整数复数常数 关于包含Euler函数φ(n)的一个方程的正整数解黑龙江大学自然科学学报(2022年1期)2022-03-29评析复数创新题中学生数理化(高中版.高考数学)(2021年11期)2021-12-21求解复数模及最值的多种方法中学生数理化(高中版.高二数学)(2021年4期)2021-07-20数系的扩充和复数的引入中学生数理化(高中版.高二数学)(2021年4期)2021-07-20复数新世纪智能(数学备考)(2020年12期)2020-03-29非齐次线性微分方程的常数变易法卷宗(2018年14期)2018-06-29方程xy=yx+1的全部正整数解中等数学(2018年12期)2018-02-16万有引力常数的测量新高考·高一物理(2016年3期)2016-05-18对一道IMO题的再研究中学数学杂志(高中版)(2014年6期)2014-11-29紫外分光光度法测定曲札芪苷的解离常数云南中医学院学报(2012年3期)2012-07-31本文来源:http://www.zhangdahai.com/shiyongfanwen/qitafanwen/2023/0612/610237.html